为什么我要放弃javaScript数据结构与算法（第十章）—— 排序和搜索算法

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 5,434

本章将会学习最常见的排序和搜索算法，如冒泡排序、选择排序、插入排序、归并排序、快速排序和堆排序，以及顺序排序和二叉搜索算法。

第十章 排序和搜索算法

排序算法

我们会从一个最慢的开始，接着是一些性能好一些的方法

先创建一个数组（列表）来表示待排序和搜索的数据结构。

1
2
3
4
5
6
7
8
9
function ArrayList(){
    var array = [];
    this.insert = function(item){
        array.push(item);
    }
    this.toString = function(){
        return array.join();
    }
}

ArrayList 是一个简单的数据结构，它将项存储在数组。我们只需要一个插入方法来向数据结构中添加元素。使用js原生的push方法即可，而改写toString函数运用了js的join方法是来拼接数组中的所有元素至一个单一的字符串。

冒泡排序

冒泡排序是所有排序算法中最简单，然后从运行时间看，它也是最差的一个、

冒泡排序比较两个相邻的项，如果第一个大于第二个，则交换它们。元素项向上移动至正确的顺序，就好像气泡升至表面一样，冒泡排序因此得名。

1
2
3
4
5
6
7
8
9
10
11
// 冒泡排序
this.bubbleSort = function(){
    var length = array.length;
    for(var i = 0; i <length; i++){
        for(var j = 0; j < length -1; j--){
            if(array[j] > array[j+1]){
                this.swap(j,j+1);
            }
        }
    }
}

首先，声明一个 名为length的变量，用来存储数组的长度。接着外循环从数组的第一位迭代到最后一位，它控制了在数组中经过多次轮排序，然后内循环将从第一位迭代到倒数第二位，内循环实际上进行当前项和下一项的比较。如果这两项顺序不对，则交换它们，意思就是位置为 j+1 的会被换到位置 j 处。

声明 swap函数

1
2
3
4
5
6
this.swap = function(index1,index2){	
    var aux = array[index1];
    array[index1] = array[index2];
    array[index2] = aux;
// [array[index1],array[index2]] = [array[index2],array[index1]]
}

交换时，我们用一个中间值来存储某一交换项的值。其他排序法也会用到这个方法，因此我们声明一个方法放置这段交换代码以便重用。

还可以简化成

1
[array[index1],array[index2]] = [array[index2],array[index1]]

下面这个示意图展示了冒泡排序的工作过程

冒泡排序

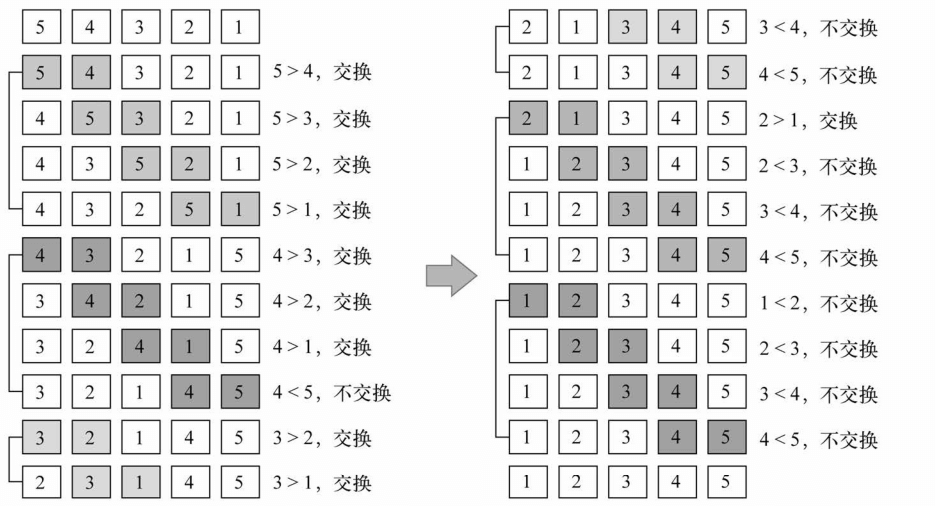
上面的图每一小段表示外循环的一轮，而相邻两项的比较是在内循环中进行的。

用下面的代码来测试冒泡排序算法

1
2
3
4
5
6
7
8
9
10
11
12
function createNonSortedArray(size){
    var array = new ArrayList();
    for(var i = size; i > 0; i--){
        array.insert(i);
    }
    return array;
}

var array = createNonSortedArray(5);
console.log(array.toString()); // 5,4,3,2,1
array.bubbleSort();
console.log(array.toString());	// 1,2,3,4,5

为了辅助本章将要学习的排序算法，我们将创建一个函数来自动地创建一个未排序的数组，数组的长度由函数的参数指定。如果传递5为参数，该函数就会创建如下数组

[5,4,3,2,1]

调用这个函数并将返回值存储在一个变量中，该变量将包含这个以某些数字来初始化的 ArrayList 类实例。

注意当算法执行外循环的第二轮的时候，数字4和5已经是正确排序的了。但是在后续的比较中，它们还是在一直进行着比较，即使这是不必要的。因此我们稍微改进一下。

改进版冒泡排序

1
2
3
4
5
6
7
8
9
10
11
// 改进后的冒泡排序
this.modifiedBubbleSort = function(){
    var length = array.length;
    for(var i = 0; i <length; i++){
        for(var j = 0; j < length-1-i; j++){
            if(array[j] > array[j+1]){							
                this.swap(j,j+1);
            }
        }
    }
}

下图展示了改进后的冒泡排序算法是如何执行的：

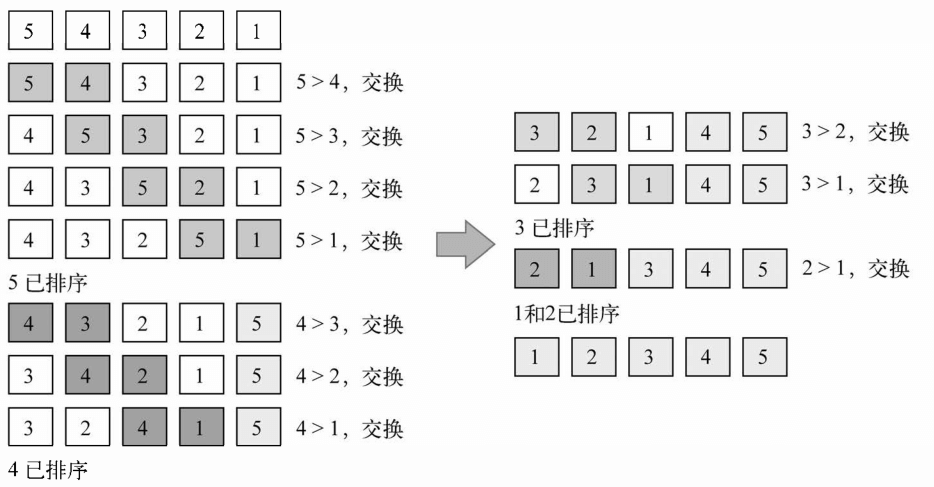
优化冒泡排序

可以通过检验知道减少了10次循环，优化了算法的性能。

即使做了这样子的改变，还是不推荐该算法，该算法的复杂度是O(n2 )

后面的章节会介绍大O表达法。

选择排序

选择排序算法是一种原址比较排序算法。选择排序大致的思路是找到数据结构中最小值并将其放置在第一位，接着找到第二小的值并将其放在第二位。以此类推。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
// 选择排序
this.selectionSort = function(){
    var length = array.length,
    indexMin;
    for(var i = 0; i < length; i++){
        indexMin = i;
        for(var j = i; j < length; j++){
            if(array[indexMin] > array[j]){
                indexMin = j;
            }
        }
        if(i !== indexMin){
            this.swap(i,indexMin);
        }
    }
}

首先声明一些将在算法内使用的变量。接着，外循环迭代数组，并控制迭代一次（数组的第n个值——下一个最小值）。我们假设本迭代一次的第一个值为数组的最小值。然后，当前 i 的值开始至数组结束，我们比较是否位置 j的值比当前的最小值小。如果是则改变最小值为新的最小值。当内循环结束，将得出数组的第n小的值。最后，如果该最小值和原最小值不一样，则交互其值。

测试：

1
2
3
4
var array = createNonSortedArray(5);
console.log(array.toString()); // 1,2,3,4,5
array.selectionSort();
console.log(array.toString());	// 1,2,3,4,5

下图的示意图展示了选择排序算法，此例基于之前的代码中所用的数组。

选择排序

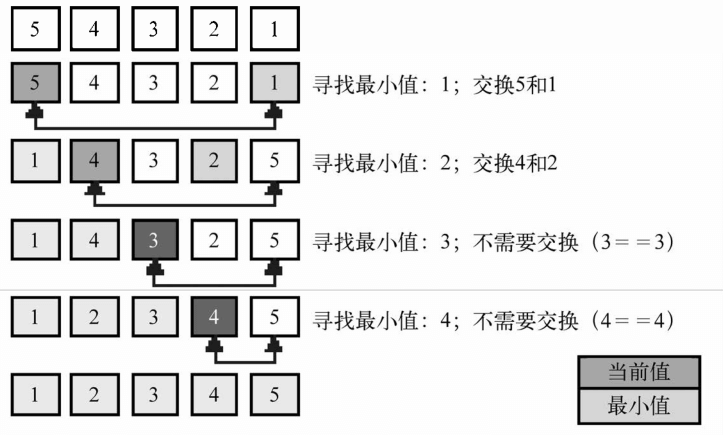
数组底部的箭头指示出了当前迭代寻找最小值的数组范围，示意图中的每一步则表示外部循环。

选择排序同样是一个复杂度也是 O(n2)的算法。和冒泡排序一样，它包含有嵌套的两个循环，这导致了二次方的复杂度。然后，接下来要学的插入排序比选择排序的性能要好。

插入排序

插入排序每次排一个数组项，以此方式构建最后的排序数组。假设第一项已经排序，接着，它和第二项进行比较，第二项是应该待在原位还是插入到第一项之前呢？这样，头两项就已经正确排序，接着和第三项比较（它是该插入到第一、第二还是第三的位置呢？），以此类推

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 插入排序
this.insertionSort = function(){
    var length = array.length,
    j,
    temp;
    for(var i = 0; i <length; i++){
        j = i;
        temp = array[i];
        while(j > 0 && array[j - 1] > temp){
            array[j] = array[j - 1]
            j--;
        }
        array[j] = temp;
    }
}

先声明代码中使用的变量，接着，迭代数组来给第i项找到正确的位置。注意，算法是从第二个位置而不是从0位置开始的。然后用i值来初始化一个辅助变量并将其保存于一临时变量中，便于之后将其插入到正确的位置上。下一步是找到正确的位置来插入项目。只要变量j比0大并且数组中前面的值比待比较的值大，我们就把这个值移到当前位置上并减小j。最终，该项目能插入到正确的位置上。

下面的示意图展示了一个插入排序的实例：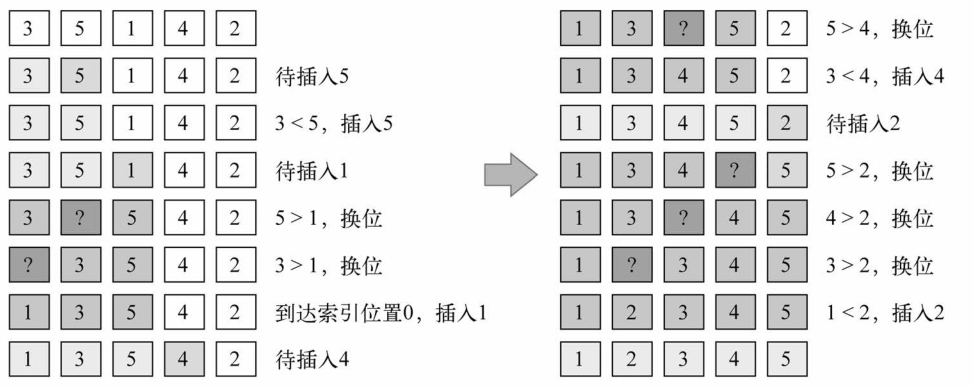
插入排序

排序小型数组时，此算法比选择排序和冒泡排序性能都要好。

归并排序

归并排序是第一个可以被实际使用的排序算法。归并排序性能复杂度为 O(nlog(n))

归并算法是一种分治算法。其思想是将原始数组切成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后一个排序完毕的大数组。

由于是分治法，归并排序也是递归的。

1
2
3
4
// 归并排序
this.mergeSort = function(){
    array = this.mergeSortRec(array);
}

mergeSortRec 是递归函数

1
2
3
4
5
6
7
8
9
10
this.mergeSortRec = function(array){
    var length = array.length;
    if(length === 1){
        return array;
    }
    var mid = Math.floor(length/2),
    left = array.slice(0,mid),
    right = array.slice(mid,length);
    return merge(arguments.callee(left),arguments.callee(right));
}

归并排序将一个大数组转化为一个小数组直到只有一个项。由于算法是递归的，我们需要一个停止条件，在这里条件是判断数组的长度是否为1.如果是，则直接返回这个长度为1的数组，因为它已经排序了。

如果数组长度比1大，那么我们得将其分成小数组。为此，首先要找到数组的中间行，找到后我们将数组分成两个小数组，分别叫做left 和 right 。 left 数组由索引0至中间索引的元素组成，而 right 数组由中间索引至原始数组最后一个位置的元素组成。

下面的步骤就是调用merge 函数，它负责合并和排序小数组来产生大数组，直到回到原始数组已排序完成。为了不断将原始数组分成小数组，我们得再次对left 数组和right 数组递归调用 mergeSortRec ，并同时作为参数传递给 merge 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function merge(left,right){
    var result = [],
    il = 0,
    ir = 0;
    while(il < left.length && ir < right.length){
        if(left[il] < right[ir]){
            result.push(left[il++]);
        }else{
            result.push(right[ir++]);
        }
    }
    while(il < left.length){
        result.push(left[il++]);
    }
    while(ir < right.length){
        result.push(right[ir++]);
    }
    return result;			
}

merge 函数接受两个数组作为参数，并将它们归并至一个大数组。排序发生在归并过程中。首先，需要声明归并过程要创建的新数组已经用来迭代两个数组（left和right数组）所需要的两个变量。迭代两个数组的过程中，我们来自left 数组的项是否比来自right的数组的项小。如果是，将该项从left数组添加至归并结果数组，并递增迭代数组的控制变量；否则，从right数组添加项并递增相应的迭代数组的控制变量。

接下来，将left数组或right数组所有剩下的项添加到归并数组中。最后，将归并数组作为结果返回。

下图是具体的执行过程

归并排序

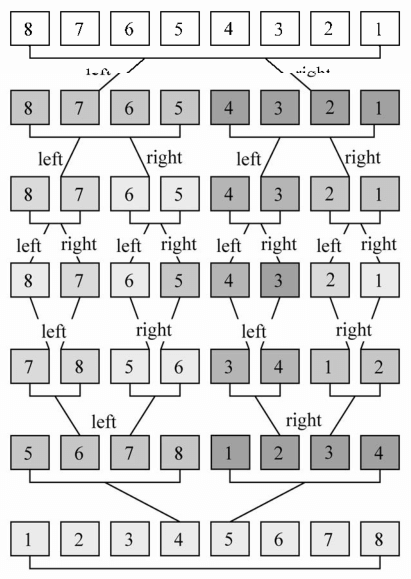
可以看到，算法首先将原始数组分割成只有一个元素的子数组，然后开始排序。归并过程也会完成排序，知道原始数组完全合并并完成排序。

快速排序

快速排序也许是最常用的排序算法了。它的复杂度为O(nlogn)，且它的性能通常比其他的复杂度为O(nlog(n))的排序算法要好。和归并算法一样，快速排序也是用分治 的方法，将原始算法分成了较小的数组（但它没有像归并排序那样将它们分割开）

快速排序比目前之前的排序算法要负责一些。

  1. 首先，从数组中选择中间一项作为主元
  2. 创建两个指针，左边一个指向数组的第一项，右边一个指向数组最后一项。移动左指针知道我们找到一个比主元大的元素，接着，移动右指针直到找到一个比主元小的元素，然后交换它们，重复这个过程，直到左指针超过了右指针。这个过程将使得比主元小的值都排在主元之前，而比主元大的值都排在主元之后。这一步叫做划分操作。
  3. 接着，算法对划分后的小数组（较主元小的值组成的子数组，以及较主元大的值组成的子数组）重复之前的两个步骤，直到数组已完全排序。

实现：

1
2
3
4
// 快速排序
this.quickSort = function(){
    this.quick(array,0,array.length-1);
}

像归并算法那样，开始我们声明一个主方法来调用递归函数，传递待排序数组，已经索引0及其最末的位置作为参数。

1
2
3
4
5
6
7
8
9
10
11
12
this.quick = function(array,left,right){
    var index;
    if(array.length > 1){
        index = partition(array,left,right);
        if(left < index - 1 ){
            arguments.callee(array,left,index-1);
        }
        if(index < right){
            arguments.callee(array,index,right);
        }				
    }
}

首先声明 index ，该变量能帮助我们将子数组分离成较小值数组和较大值数组，这样，我们就能再次递归的调用quick函数了。partition 函数返回值将赋值给 index.

如果数组的长度比1大，我们就对给定子数组执行 partition 操作以得到 index 。如果子数组存在较小值的元素，则对该数组重复这个过程。同理，对存在较大值的子数组也是如此。

划分过程

第一件要做的事情就是选中主元（pivot）,有好几种方式，最简单的一种就是选中数组的第一项（最左项）。然而，研究表明对于几乎已排序的数组，这不是一个好的选择，它将导致该算法的最差表现。另外一种方式是随机选择一个数组或是选择中间项。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function partition(array,left,right){
    var pivot = array[Math.floor((left+right) / 2)],
    i = left,
    j = right;
    while(i <= j){
        while(array[i] < pivot){
            i++
        }
        while(array[j] > pivot){
            j--
        }
        if(i <= j){
            [array[i],array[j]] = [array[j],array[i]];
            i++;
            j--
        }
    }
    return i;
}

上面的实现中，我们选中中间项作为主元。我们初始化两个指针：left，初始化为数组第一个元素，right，初始化为数组最后一个元素。

只要left和right指针没有相互交错，就执行划分操作。首先，先移动left指针直到找到一个元素比主元大。对于right指针，我们做同样的事情，移动right指针直到我们找到一个元素比主元小。

当左指针指向的元素比主元大且右指针指向的元素比主元小，并且此时左指针索引没有右指针索引大，意思是左项比右项大。我们交换它们，然后移动两个指针，并重复这个过程。

在划分操作结束后，返回左指针的索引，用来在创建子数组。

快速排序实战

看一个快速排序的实际例子

快速排序

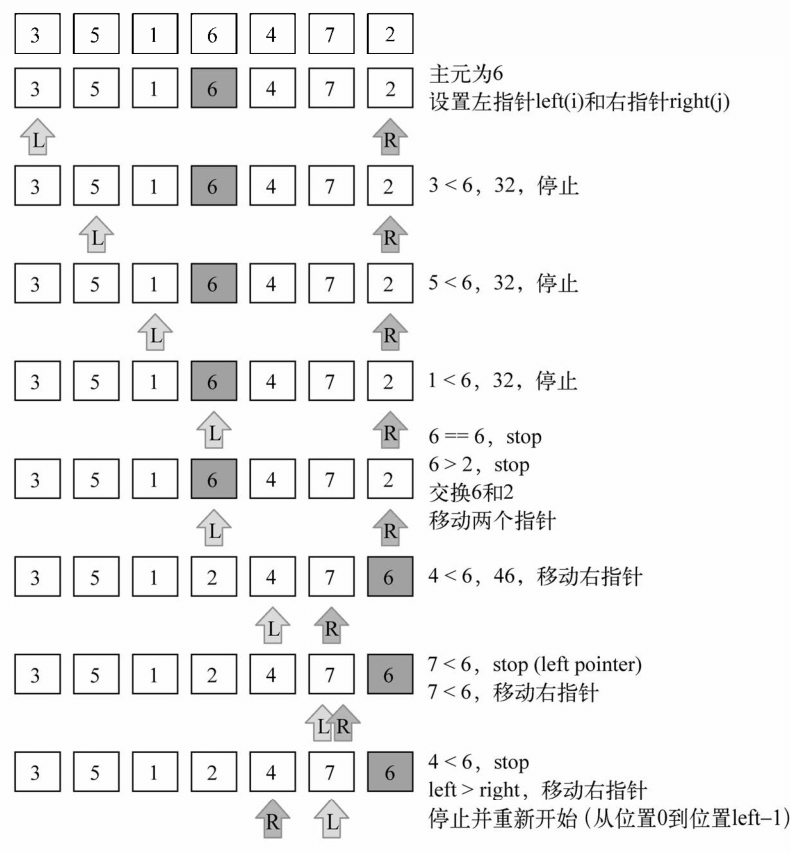
给定数组（[3,5,1,6,4,7,2]），前面的示意图展示了划分操作的第一次执行。

下面的示意图展示了对有较小值的子数组执行的划分（注意7和6不包含在子数组之内）

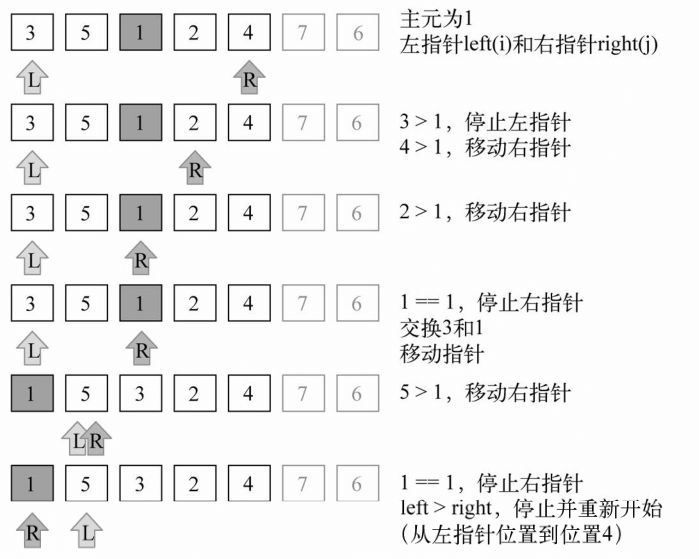
快速排序2

接着，我们继续创建子数组，但是这次操作是针对上图中有较大值的子数组（有1那个较小数组不用再划分了，因为它仅含有一个项）

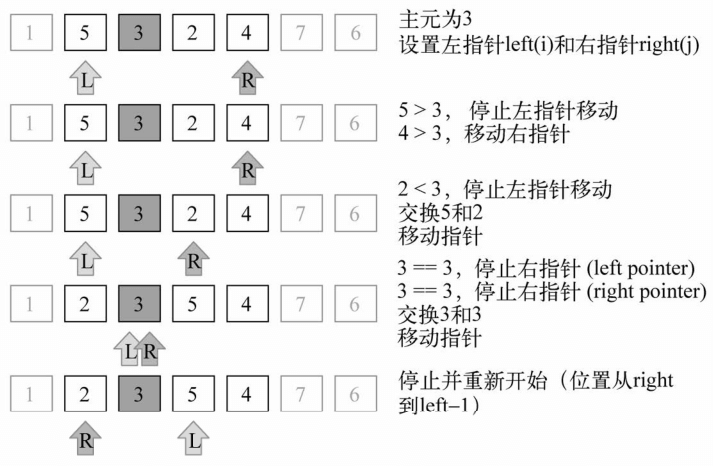
快速排序3

子数组（[2,3,5,4]）中的较小数组（[2,3]）继续划分。

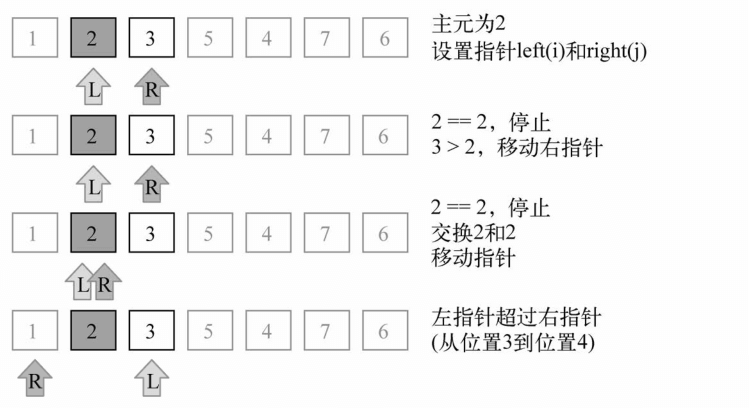
快速排序4

然后子数组（[2,3,5,4]）中较大数组（[5,4]）也继续进行划分，示意图如下

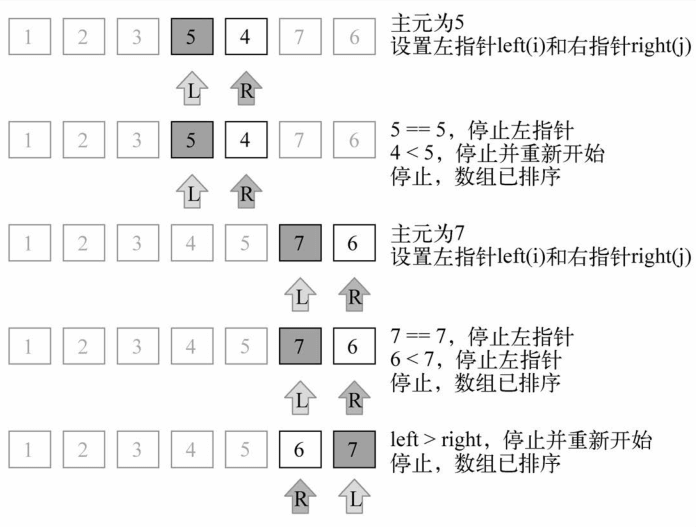
快速排序5

最终，较大子数组（[6,7]）也会进行继续划分操作，快速排序算法的操作执行完成。

计数排序、桶排序和基数排序（分布式排序）

目前为止，已经学习了如何不借助任何辅助数据结构的情况下对数组进行排序。还有一类被称为分布式排序的算法，原始数组中的数据会分发到多个中间结构（桶），再合起来放回原始数组。

最著名的分布式算法有计数排序、桶排序和基数排序。这里不做展开，有兴趣的请自行百度。

排序的相关代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
function createNonSortedArray(size){
    var array = new ArrayList();
    for(var i = size; i > 0; i--){
        array.insert(i);
    }
    return array;
}
function merge(left,right){
    var result = [],
    il = 0,
    ir = 0;
    while(il < left.length && ir < right.length){
        if(left[il] < right[ir]){
            result.push(left[il++]);
        }else{
            result.push(right[ir++]);
        }
    }
    while(il < left.length){
        result.push(left[il++]);
    }
    while(ir < right.length){
        result.push(right[ir++]);
    }
    return result;			
}
function partition(array,left,right){
    var pivot = array[Math.floor((left+right) / 2)],
    i = left,
    j = right;
    while(i <= j){
        while(array[i] < pivot){
            i++
        }
        while(array[j] > pivot){
            j--
        }
        if(i <= j){
            [array[i],array[j]] = [array[j],array[i]];
            i++;
            j--
        }
    }
    return i;
}
function ArrayList(){
    var array = [];
    this.insert = function(item){
        array.push(item);
    }
    this.toString = function(){
        return array.join();
    }
    this.swap = function(index1,index2){	
        var aux = array[index1];
        array[index1] = array[index2];
        array[index2] = aux;
    // [array[index1],array[index2]] = [array[index2],array[index1]]
    }			
    // 冒泡排序
    this.bubbleSort = function(){
        var length = array.length;
        for(var i = 0; i <length; i++){
            for(var j = 0; j < length -1; j++){
                if(array[j] > array[j+1]){								
                    this.swap(j,j+1);
                }
            }
        }
    }
    // 改进后的冒泡排序
    this.modifiedBubbleSort = function(){
        var length = array.length;
        for(var i = 0; i <length; i++){
            for(var j = 0; j < length-1-i; j++){
                if(array[j] > array[j+1]){							
                    this.swap(j,j+1);
                }
            }
        }
    }
    // 选择排序
    this.selectionSort = function(){
        var length = array.length,
        indexMin;
        for(var i = 0; i < length; i++){
            indexMin = i;
            for(var j = i; j < length; j++){
                if(array[indexMin] > array[j]){
                    indexMin = j;
                }
            }
            if(i !== indexMin){
                this.swap(i,indexMin);
            }
        }
    }
    // 插入排序
    this.insertionSort = function(){
        var length = array.length,
        j,
        temp;
        for(var i = 0; i <length; i++){
            j = i; 
            temp = array[i]; 
            while(j > 0 && array[j - 1] > temp){
                array[j] = array[j - 1]
                j--;
            }
            array[j] = temp;
        }
    }
    // 归并排序
    this.mergeSort = function(){
        array = this.mergeSortRec(array);
    }
    this.mergeSortRec = function(array){
        var length = array.length;
        if(length === 1){
            return array;
        }
        var mid = Math.floor(length/2),
        left = array.slice(0,mid),
        right = array.slice(mid,length);
        return merge(arguments.callee(left),arguments.callee(right));
    }
    // 快速排序
    this.quickSort = function(){
        this.quick(array,0,array.length-1);
    }
    this.quick = function(array,left,right){
        console.log(left+'  '+right);
        var index;
        if(array.length > 1){
            index = partition(array,left,right);
            if(left < index - 1 ){
                arguments.callee(array,left,index-1);
            }
            if(index < right){					
                arguments.callee(array,index,right);
            }				
        }
    }
}

// var array = createNonSortedArray(5);
// console.log(array.toString());
// array.quickSort();
// console.log(array.toString());	
const quickSortArray = new ArrayList();
quickSortArray.insert(3);
quickSortArray.insert(5);
quickSortArray.insert(1);
quickSortArray.insert(6);
quickSortArray.insert(4);
quickSortArray.insert(7);
quickSortArray.insert(2);
console.log(quickSortArray.toString());
quickSortArray.quickSort();
console.log(quickSortArray.toString());

搜索算法

回顾一下之前学过的算法，我们会发现BinarySearch Tree 类的search以及LinkedList类的indexOf 方法等都是搜索算法。当然，它们都是根据各自的数据结构来实现的。所以我们其实已经熟悉两个搜索算法了，只是还不知道它们的正式名称而已。

顺序搜索

顺序或者线性搜索是基本的搜索算法。它的机制是，将每一个数据结构中的元素和我们要找的元素做比较。顺序搜索是最低效的一种搜索算法。

1
2
3
4
5
6
7
8
9
// 顺序搜索
this.sequentialSearch = function(item){
    for(var i = 0; i < array.length; i++){
        if(item === array[i]){
            return i;
        }
    }
    return -1;
}

顺序搜索迭代整个数组，并将每个数组元素和搜索项作比较。如果搜索到了，算法将返回值来标示搜索成功。返回值可以是该搜索项本身，或是true,又或是搜索项的索引。如果没有找到该项，则返回-1，表示该索引不存在，也可以考虑返回false或者null。

假定有数组（[5,4,3,2,1]）和待搜索值3，下图展示了顺序搜索的示意图

顺序搜索

二分搜索

二分搜索算法的原理和菜数字游戏类似。我们每回应一个数字。那个人就会说这个数字是高了还是低了或者是对了。

这个算法要求被搜索的数据结构已经排序。以下是该算法遵循的步骤

  1. 选择数组的中间值
  2. 如果选中值是待搜索值，那么算法执行完毕
  3. 如果待搜索值比选中的小，则返回步骤1并在选中值的左边的子数组中寻找
  4. 如果待搜索值比选中的大，则返回步骤1并在选中值的右边的子数组中寻找

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 二分搜索
this.binarySearch = function(item){
    this.quickSort();
    var low = 0,
    high = array.length - 1,
    mid,element;
    while(low <= high){
        mid = Math.floor((low + high)/2);
        element = array[mid];
        if(element < item){
            low = mid + 1;
        }else if(element > item){
            high = mid - 1;
        }else{
            return mid;
        }
    }
    return -1;
}

开始前需要先排序数组，我们这这里选择了快速排序。在数组排序之后，我们设置low和high指针（它们是边界）

当low比high小时，我们计算得到中间项索引并取得中间项的值，此处如果low比high大，则意思是该搜索值不存在并返回-1.接着，我们比较选中项的值和搜索值。如果小了，则选择数组低半边并重新开始。如果选中项的值比搜索值大了，则选择数组高半边并重新开始。若两者都不是，则意味着选中项的值和搜索值相等，因此，直接返回该索引。

给定下图所示数组，试试搜索2.这是算法将会执行的步骤：

顺序搜索

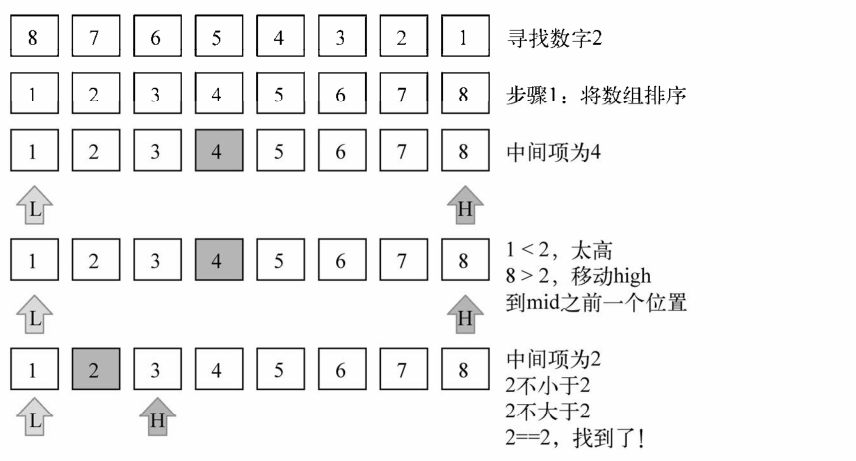
小结

本章介绍了排序和搜索算法，包括冒泡、选择、插入、归并和快速排序，还有顺序搜索和二分搜索。下一章学习一些高级算法技巧。

书籍链接： 学习JavaScript数据结构与算法

0%