为什么我要放弃javaScript数据结构与算法（第十一章）—— 算法模式

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 4,342

本章将会学习递归、动态规划和贪心算法。

第十一章 算法模式

递归

递归是一种解决问题的方法，它解决问题的各个小部分，直到解决最初的大问题。递归通常涉及函数调用自身。

递归函数是像下面能够直接调用自身的方式或函数

1
2
3
function recursiveFunction(someParam){
    recursiveFunction(someParam);
}

能够像下面这样间接调用自身的函数，也是递归函数

1
2
3
4
5
6
function recursiveFunction1(someParam){
    recursiveFunction2(someParam);
}
function recursiveFunction2(someParam){
    recursiveFunction1(someParam);
}

假设现在必须要执行 recursiveFunction ,结果是什么?单单上述情况而言，它会一直执行下去。因此，每个递归函数都必须有边界条件，即一个不再递归调用的条件（停止点），以防无限递归。

JavaScript 调用栈大小的限制

如果忘记加上用以停止函数递归调用的边界条件，会发生什么呢？递归并不会无限执行下去，浏览器会抛出错误，也就是所谓的栈溢出错误（stack Overflow error）

每个浏览器都有自己的上限，可以用一下代码测试。

1
2
3
4
5
6
7
8
9
10
11
12
13
var i = 0;
function recursiveFn(){
    i++;
    recursiveFn();
}
try{
   recursiveFn(); 
}catch(e){
    console.log('i='+i+' error:'+e);
}
// 谷歌：i=15706 error:RangeError: Maximum call stack size exceeded
// 360：i=31470 error:RangeError: Maximum call stack size exceeded
// 火狐：i=40687 error:InternalError: too much recursion

根据操作系统和浏览器的不同，具体的数值也会有所不同，但区别不大。

ES6 有尾调用优化（tail call optimazation）。如果函数内最后一个操作是调用函数，会通过“跳转指令（jump）”而不是“子程序调用（subroutine call ）”来控制。也就是说，ES6中，这里的代码会一直执行下去。所以，具有停止递归的边界条件很重要。

尾调用 点击看看，阮一峰老师的。

斐波那契数列

斐波那契数列的定义如下：

  • 1 和 2 的斐波那契数是1
  • n（n>2）的斐波那契数是（n-1）加上（n-2）的斐波那契数。

实现

1
2
3
4
5
6
function fibonacci(num){
    if(num === 1 || num ===2){
        return 1;
    }
    return arguments.callee(num - 1) + arguments.callee(num - 2);
}

让我们试着找出6的斐波那契数，其会产生如下函数调用

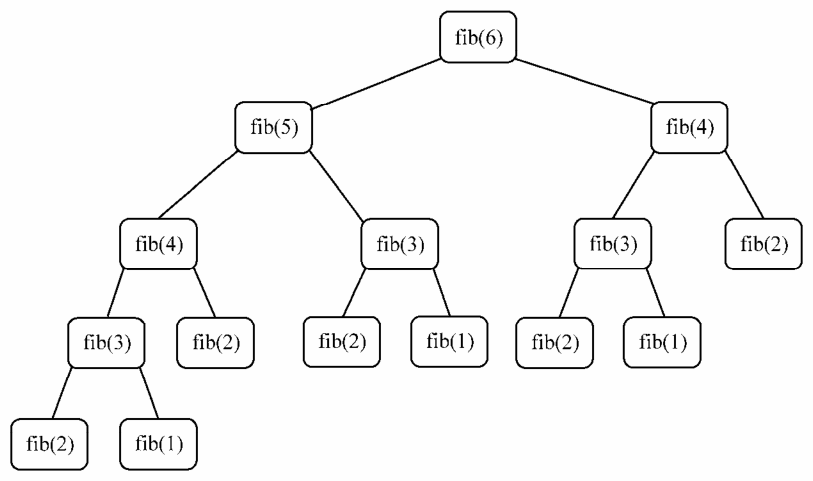
斐波那契函数

我们也可以用非递归的方法实现

1
2
3
4
5
6
7
8
9
10
11
function fib(num){
    var n1 = 1,
    n2 = 1,
    n = 1;
    for(var i = 3; i <= num; i++){
        n = n1 + n2;
        n1 = n2;
        n2 = n;
    }
    return n;
}

为什么要用递归？是因为更快吗？其实并不，反而更慢。递归的好处在于更容易理解，并且它所需的代码量更少。然后在ES6中，因为有尾调用，可以加快递归的速度。总而言之，我们用递归，通常是因为它更容易解决问题。

动态规划

动态规划（Dynamic Programming,DP）是一种将复杂问题分解成更小的子问题来解决的优化技术。与分而治之不同的是，动态规划是将问题分解成相互依赖的子问题。

用动态规划解决问题，要遵循三个步骤：

  1. 实现子问题。
  2. 实现要反复执行来解决子问题的部分
  3. 识别并求解出边界条件

可以用动态规划解决一些著名的问题如下：

  • 背包问题：给出一组项目，各自有值和容量，目标是要找出总值最大的项目的集合。这个问题的限制是，总容量必须小于等于“背包”的容量。
  • 最长公共子序列：找出一组序列的最长公共子序列（可由另一序列删除元素但不改变）
  • 矩阵链相乘：给出一系列矩阵，目标是找到这些矩阵相乘的最高效办法（计算次数尽可能少）。相乘操作不会进行，解决方案是找到这些矩阵各自相乘的顺序。
  • 硬币找零：给出面额为d1…dn的一定数量的硬币和要找零的钱数，找出有多少种找零的方法。
  • 图的全源最短路径：对所有顶点对（u,v），找出顶点u到顶点v的最短路径。

最少硬币找零问题

最少硬币找零问题是硬币问题的一个变种。硬币找零问题是给出要找零的钱数，以及可以用的硬币面额d1…dn 及其数量，找出有多少种找零方法。最少硬币找零问题是要给出要找零的钱数以及可用的硬币面额d1…dn及其数量，找出所需的最少硬币个数。

例如，美国有一下面额（硬币）：d1=1,d2=5,d3=10,d4=25

如果要找36美分的零钱，我么可以用1个25美分，1个10美分和一个便士（1美分）

如何将这个解答转化成算法？

最少硬币找零的解决方案是找到n所需的最小硬币数。但要做到这一点，首先得找到对每个x<n的解。然后，我们将解建立在更小的值的基础上。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
function MinCoinChange(coins){
    var coins = coins; // 零钱的面额
    var cache = {}; // 缓存
    this.makeChange = function(amount){ // 递归函数
        var me = this;
        if(!amount){ // 若金额总额小于0则返回空数组
            return [];
        }
        if(cache[amount]){ // 若缓存中已有该计算结果，则直接返回 
            return cache[amount];
        }
        var min = [],newMin,newAmount; 
        for(var i = 0; i < coins.length; i++){
            var coin = coins[i];
            newAmount = amount - coin;
            if(newAmount >= 0){
                newMin = me.makeChange(newAmount);					
            }
            if(newAmount >= 0 && (newMin.length < min.length - 1 || !min.length) && (newMin.length || !newAmount)){
                min = [coin].concat(newMin);
                console.log('new Min '+ min + 'for '+ amount);
            }
        }
        return (cache[amount] = min);
    }
    this.getCache = function(){
        console.log(cache);
    }
}

测试

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
const minCoinChange = new MinCoinChange([1,5,10,25]);
console.log(minCoinChange.makeChange(36));
/*
new Min 1,1,1,1,1for 5
new Min 5for 5
new Min 1,5for 6
new Min 1,1,5for 7
new Min 1,1,1,5for 8
new Min 1,1,1,1,5for 9
new Min 1,1,1,1,1,5for 10
new Min 5,5for 10
new Min 10for 10
new Min 1,10for 11
new Min 1,1,10for 12
new Min 1,1,1,10for 13
new Min 1,1,1,1,10for 14
new Min 1,1,1,1,1,10for 15
new Min 5,10for 15
new Min 1,5,10for 16
new Min 1,1,5,10for 17
new Min 1,1,1,5,10for 18
new Min 1,1,1,1,5,10for 19
new Min 1,1,1,1,1,5,10for 20
new Min 5,5,10for 20
new Min 10,10for 20
new Min 1,10,10for 21
new Min 1,1,10,10for 22
new Min 1,1,1,10,10for 23
new Min 1,1,1,1,10,10for 24
new Min 1,1,1,1,1,10,10for 25
new Min 5,10,10for 25
new Min 25for 25
new Min 1,25for 26
new Min 1,1,25for 27
new Min 1,1,1,25for 28
new Min 1,1,1,1,25for 29
new Min 1,1,1,1,1,25for 30
new Min 5,25for 30
new Min 1,5,25for 31
new Min 1,1,5,25for 32
new Min 1,1,1,5,25for 33
new Min 1,1,1,1,5,25for 34
new Min 1,1,1,1,1,5,25for 35
new Min 5,5,25for 35
new Min 10,25for 35
new Min 1,10,25for 36 
(3) [1, 10, 25]
*/
minCoinChange.getCache();	
// {1: Array(1), 2: Array(2), 3: Array(3), 4: Array(4), 5: Array(1), 6: Array(2), 7: Array(3), 8: Array(4), 9: Array(5), 10: Array(1), 11: Array(2), 12: Array(3), 13: Array(4), 14: Array(5), 15: Array(2), 16: Array(3), 17: Array(4), 18: Array(5), 19: Array(6), 20: Array(2), 21: Array(3), 22: Array(4), 23: Array(5), 24: Array(6), 25: Array(1), 26: Array(2), 27: Array(3), 28: Array(4), 29: Array(5), 30: Array(2), 31: Array(3), 32: Array(4), 33: Array(5), 34: Array(6), 35: Array(2), 36: Array(3)}

const minCoinChange1 = new MinCoinChange([1,3,4]);
console.log(minCoinChange1.makeChange(6));
/*
 new Min 1for 1
 new Min 1,1for 2
 new Min 1,1,1for 3
 new Min 3for 3
 new Min 1,3for 4
 new Min 4for 4
 new Min 1,4for 5
 new Min 1,1,4for 6
 new Min 3,3for 6
 (2) [3, 3]
*/
minCoinChange1.getCache();	// {1: Array(1), 2: Array(2), 3: Array(1), 4: Array(1), 5: Array(2), 6: Array(2)}

背包问题

背包问题是一个组合优化问题。它可以描述如下：给定一个固定大小、能够携带W的背包，以及一组有价值和重量的物品，找出一个最佳解决方案，使得装入背包的物品总重量不超过W，且总价值最大。

下面是一个例子：

物品 重量 价值
1 2 3
2 3 4
3 4 5

考虑背包能够携带的重量只有5。对于这个例子，我们可以说最佳解决方案就是往背包里装入物品1和物品2，这样，总重量为5，总价值为7。

背包算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function knapSack(capacity,weights,values,n){
    var i,w,a,b,kS = [];
    for(i = 0; i <= n; i++){
        kS[i] = [];
    }
    for(i = 0; i <= n; i++){
        for(w = 0; w <= capacity; w++){
            if(i == 0 || w == 0){
                kS[i][w] = 0;
            }else if(weights[i-1] <= w){
                a = values[i - 1] + kS[i - 1][w - weights[i-1]];
                b = kS[i-1][w];
                kS[i][w] = (a > b) ? a : b;
            }else{
                kS[i][w] = kS[i-1][w];
            }
        }
    }
    return kS[n][capacity];
}

工作原理

  • 首先，初始化将用于寻找解决方案的矩阵ks[n+1][capacity+1]
  • 忽略矩阵的第一列和第一行，只处理索引不为0的列和行
  • 物品i的重量必须小于约束（capacity）才有可能成为解决方案的一部分。否则，总重量就会超出背包能够携带的重量。发生这种情况的话，就采用之前的值。
  • 当找到可以构成解决方案的物品时，选择价值最大的那个
  • 问题的解决方案就在二维表格右下角的最后一个格子里面

测试

1
2
3
4
5
var values = [3,4,5],
weights = [2,3,4],
capacity = 5,
n = values.length;
console.log(knapSack(capacity,weights,values,n)); // 7

上面的算法只输出背包携带物品价值的最大值，而不列出实际的物品。我们可以增加下面的附加函数来找出构成解决方案的物品：

1
2
3
4
5
6
7
8
9
10
11
12
13
function findValues(n,capacity,kS,weights,values){
    var i = n, k = capacity;
    console.log('解决方案包含以下物品： ');
    while( i > 0 && k > 0 ){
        if(kS[i][k] !== kS[i-1][k]){
            console.log('物品' + i + '，重量：' + weights[i-1] + '，价值：'+values[i - 1] );
            i--;
            k = k - kS[i][k];
        }else{
            i--;
        }
    }
}

输出结果：

1
2
3
解决方案包含以下物品： 
物品2，重量：3，价值：4
物品1，重量：2，价值：3

最长公共子序列

另一个经常被当做编程挑战问题的动态最长公共子序列（LCS）:找出两个字符串序列的最长子序列的长度。最长子序列是指，在两个字符串序列中以相同顺序出现，但不要求连续（非字符串子串）的字符串序列。

考虑如下的例子：

字符串 元素
字符串1 a c b a e d
字符串2 a b c a d f

LCS:长度为4的‘’acad“

下面的算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
function lcs(wordX,wordY){
    var m = wordX.length,
    n = wordY.length,
    l = [],
    solution = [],
    i, j, a, b;
    for(i = 0; i <= m; ++i){
        l[i] = [];
        solution[i] = [];
        for(j = 0; j <= n; ++j){
            l[i][j] = 0;
            solution[i][j] = '0';
        }
    }
    for(i = 0; i <= m; i++){
        for(j = 0; j <= n; j++){
            if(i == 0 || j == 0){
                l[i][j] = 0;
            }else if(wordX[i-1] == wordY[j-1]){
                l[i][j] = l[i-1][j-1] + 1;
                solution[i][j] = 'diagonal';

            }else{
                a = l[i-1][i];
                b = l[i][j-1];
                l[i][j] = a > b ? a : b;
                solution[i][j] = l[i][j] == l[i-1][j] ? 'top' : 'left';
            }
        }
    }
    printSolution(solution,l,wordX,wordY,m,n);
    return l[m][n];
}

function printSolution(solution,l,wordX,wordY,m,n){
    var a = m,
        b = n,
        i,
        j,
        x = solution[a][b],
        answer = '';
        while(x !== '0'){
            if(solution[a][b] === 'diagonal'){
                answer = wordX[a-1] + answer;
                a--;
                b--;
            }else if(solution[a][b] === 'left'){
                b--;
            }else if(solution[a][b] === 'top'){
                a--;
            }
            x = solution[a][b];
        }
        console.log('lcs:' + answer);
}

矩阵链相乘（未完成）

贪心算法（未完成）

最少硬币找零问题

背包问题

函数式编程简介

借助ES6的能力，JavaScript 也能够进行函数式编程

函数式编程和命令式编程

以函数式方式进行开发并不简单。

假如我们想打印一个数组中所有的元素。我们可以用命令式编程，声明的函数如下:

1
2
3
4
5
6
var printArray = function(array){
    for(var i = 0; i < array.length; i++){
        console.log(array[i]);
    }
}
printArray([1,2,3,4,5]);

在上面的代码中，我们迭代数组，打印每一项。

现在，我们试着将这个例子转换成函数式编程。在函数式编程中，我们关注的重点是需要描述什么，而不是如何描述

1
2
3
4
5
var forEach = function(array,action){
    for(var i = 0; i < array.length; i++){
        action(array[i]);
    }
}

接着我们需要创建另一个元素负责把数组元素打印到控制台的函数（考虑为回调函数），如下

1
2
3
var logItem = function(item){
    console.log(item);
}

最后，像下面这样使用函数

1
forEach([1,2,3,4,5],logItem);

几点需要注意：

  • 主要目标是描述数据，已经要对数据应用的转换
  • 程序执行顺序的重要性很低，而在命令式编程中，步骤和顺序是非常重要的
  • 函数和数据结合是函数式编程的核心
  • 在函数式编程中，我们可以使用和滥用函数和递归，而在命令式编程中，则使用循环、赋值、条件和函数。

另外一个例子，考虑我们要找数组中最小的值。用命令式编程完成这个任务，只要迭代数组，检查当前的最小值是否大于数组元素，如果是，就更行最小值。

1
2
3
4
5
6
7
8
9
10
var findMinArray = function(array){
    var minValue = array[0];
    for(var i = 1; i < array.length; i++){
        if(minValue > array[i]){
           minValue = array[i];
        }
    }
    return minValue;
}
console.log(findMinArray([8,6,4,5,9])); // 4

用函数式编程完成相同的任务，可以使用Math.in 函数，传入所有要比较的数组元素。我们可以像下面的例子里这样，使用ES2015 的解构操作符（…）,把数组转换成单个元素：

1
2
3
4
const min_ = function(array){
    return Math.min(...array);
}
console.log(min_([8,6,4,5,9])); // 4

使用箭头函数，简化代码

1
const min_ = arr => Math.min(...arr);

JavaScript函数式工具箱——map、filter 和 reduce

map、filter和reduce函数是函数式编程的基础

我们可以使用map函数 ，把一个数据集合转换成映射成另一个数据集合。先看一个命令式编程的例子：

1
2
3
4
5
6
7
8
9
var daysOfWeek = [
    { name: 'Monday', value: 1 },
    { name: 'Tuseday', value: 2 },
    { name: 'Webnesday', value: 7 },
]
var daysOfWeekValues_ = [];
for(var i = 0; i < daysOfWeek.length; i++ ){
    daysOfWeekValues_.push(daysOfWeek[i].value);
}

再以函数式编程来考虑同样的例子，代码如下：

1
2
3
4
var daysOfWeekValues = daysOfWeek.map(function(day){
    return day.value;
})
console.log(daysOfWeekValues);

我们可以使用 filter 函数过滤一个集合的值。来看一个例子

1
2
3
4
5
6
7
8
9
10
var positiveNumbers_ = function(array){
    var positive = [];
    for(var i = 0; i < array.length; i++){
        if(array[i] >= 0){
           positive.push(array[i]);
        }
    }
    return positive;
}
console.log(positiveNumbers_([-1,1,2,-2])); // (2) [1, 2]

改成函数式

1
2
3
4
5
6
var positiveNumbers = function(array){
    return array.filter(function(num){
        return num >= 0;
    });
}
console.log(positiveNumbers([-1,1,2,-2])); // (2) [1, 2]

也可以使用reduce函数，把一个集合归纳成一个约定的值。比如，对一个数组中的值求和：

1
2
3
4
5
6
7
8
var sumValues = function(array){
    var total = array[0];
    for(var i = 1; i < array.length; i++){
        total += array[i];
    }
    return total;
}
console.log(sumValues([1,2,3,4,5])); // 15

上面的代码也可以写成这样的：

1
2
3
4
5
6
var sum_ = function(array){
    return array.reduce(function(a,b){
        return a + b;
    });
}
console.log(sum_([1,2,3,4,5])); // 15

再看另外一个例子，考虑我们需要写一个函数，把几个数组连接起来。为此，可以创建另外一个数组，用于存放其他数组的元素。我们可以执行以下命令式的代码

1
2
3
4
5
6
7
8
9
10
11
12
var mergeArrays = function(arrays){
    var count = arrays.length,
        newArray = [],
        k = 0;
    for(var i = 0; i < count; i++){
        for(var j = 0; j < arrays[i].length; j++){
            newArray[k++] = arrays[i][j];
        }
    }
    return newArray;
}
console.log(mergeArrays([[1,2,3],[4,5],[6]])); // (6) [1, 2, 3, 4, 5, 6]

在这个例子，我们声明了变量，还使用了循环。现在，我们用JavaScript 函数式编程把上面的代码重写如下：

1
2
3
4
5
6
var mergeArraysConcat = function(arrays){
    return arrays.reduce(function(p,n){
        return p.concat(n);
    });
}
console.log(mergeArraysConcat([[1,2,3],[4,5],[6]])); // (6) [1, 2, 3, 4, 5, 6]

箭头函数简写

1
2
const mergeArrays = (...arrays) => [].concat(...arrays);
console.log(mergeArrays([1,2,3],[4,5],[6])); // (6) [1, 2, 3, 4, 5, 6]

小结

在本章中，你了解了更多的递归的知识，已经它帮助我们解决一些动态规划问题。我们介绍了最著名的动态规划问题，如最少硬币找零、背包问题、最长公共子序列和矩阵链相乘(后面补)。

还学习了贪心算法，已经如何用贪心算法解决最少硬币找零和背包问题。

还学习了函数式编程，并通过一些例子了解了如何以这种范式使用JavaScript 的功能。

书籍链接： 学习JavaScript数据结构与算法

0%