为什么我要放弃javaScript数据结构与算法（第十二章）—— 算法复杂度

发表于 | 更新于: | 分类于 | 阅读次数:
字数统计: 1,418

花了一个星期，终于看到这本书的最后一章了。这章将要学习著名的大O表示法。

第十二章 算法复杂度

大O表示法

它用于描述算法的性能和复杂程度

分析算法时，时常遇到以下几类函数

符号 名称
O(1) 常数的
O(log(n)) 对数的
O((log(n)c)) 对数多项式的
O(n) 线性的
O(n2) 二次的
O(nc) 多项式的
O(cn) 指数的

理解大O表示法

如何衡量算法的效率？通常是用资源，例如CPU（时间）占用、内存占用、硬盘占用和网络占用。当讨论大O表示法时，一般考虑的是CPU（时间）占用。

让我们试着用一些例子来理解大O表示法的规则

O(1)

1
2
3
function increment(num){
    return ++num;
}

假设运行increment（1）函数，执行时间等于 X。如果再用不同的参数运行一次increment函数，执行事件依然是 X。和参数无关，increment函数的性能都一样。因此，我们说上述函数的复杂程度是O(1)（常数）

O(n)

1
2
3
4
5
6
7
8
function sequentialSearch(array,item){
    for(var i = 0; i < array.length; i++){
        if(item === array[i]){
        	return i;   
        }
    }
    return -1;
}

如果将含有10个元素的数组（[1,…,10]）传递给该函数，例如搜索1这个元素，那么第一次判断时就能找到想要搜索的元素。在这里我们假设每执行一次（item === array[i]）开销为1.

现在，假如要搜索元素11.那么函数会执行10次（遍历数组中所有的值，并且找不到要搜索的元素，因此结果返回-1），那么开销就是10。以此类推，sequentialSearch 函数执行的总开销取决了数组元素的个数（数组的大小）。可以得到sequentialSearch函数的时间复杂度为O(n)，n是（输入）数组的大小。

回到之前的例子，修改一下算法的实现。

1
2
3
4
5
6
7
8
9
10
function sequentialSearch(array,item){
    var cost = 0;
    for(var i = 0; i < array.length; i++){
        if(item === array[i]){
        	return i;   
        }
    }
    console.log('cost for sequentialSearch with inpy size ' + array.length + 'is' + cost);
    return -1;
}

用不同大小输入数组执行以上算法，可以看到不同的输出。

O(n2)

用冒泡排序做例子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function swap(array, index1, index2){
    var aux = array[index1];
    array[index1] = array[index2];
    array[index2] = aux;
}

function bubbleSort(array){
    var length = array.length,
        cost = 0;
    for(var i = 0; i < length; i++){
        cost++;
        for(var j = 0; j < length; j++){
            cost++;
            if(array[j] > array[j+1]){
               swap(array, j, j+1);
            }
        }
    }
    console.log('cost for bubbleSort with input size' + length + 'is' + cost);
}

如果用大小为10的数组执行上面的函数，开销是100（102）。

时间复杂度O(n)的代码只有一层循环，而O(n2)有两层循环。如果算法有三层遍历数组的嵌套循环，它的时间复杂度很有可能是O(n3)

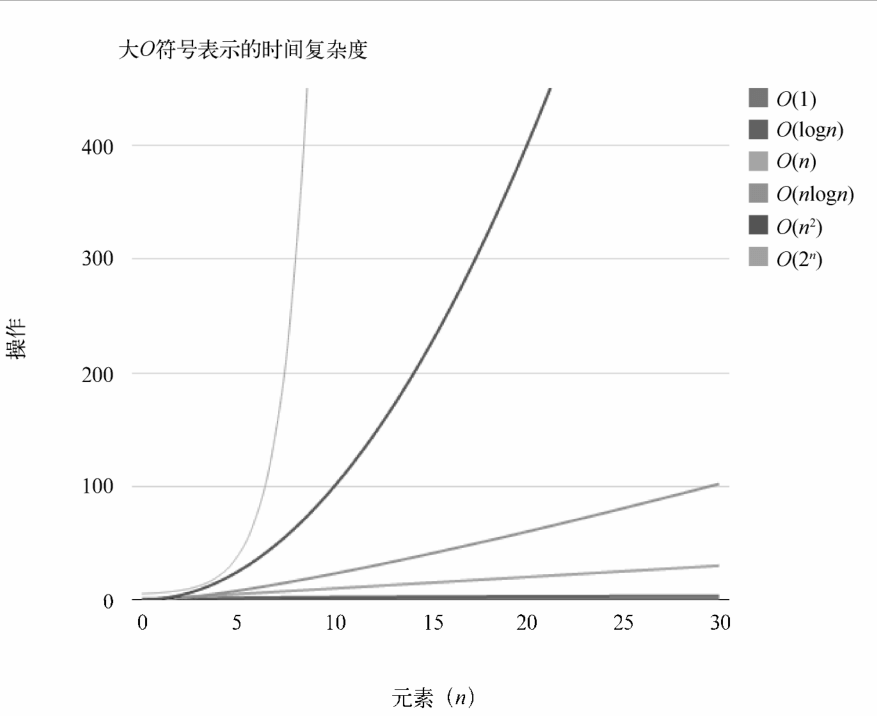
时间复杂度比较

下面比较了前述各个大O符号表示的时间复杂度

时间复杂度比较

数据结构

下表是常用数据结构的时间复杂度

数据结构 一般情况 最差情况
插入 删除 搜索 插入 删除 搜索
数组-栈-队列 O(1) O(1) O(n) O(1) O(1) O(n)
链表 O(1) O(1) O(n) O(1) O(1) O(n)
双向链表 O(1) O(1) O(n) O(1) O(1) O(n)
散列表 O(1) O(1) O(1) O(n) O(n) O(n)
二分搜索树 O(log(n)) O(log(n)) O(log(n)) O(n) O(n) O(n)
AVL树 O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n)) O(log(n))

图

下表是图的时间复杂度

节点-边的管理方式 存储空间 增加顶点 增加边 删除顶点 删除边 轮询
邻接表 O(V+E) O(1) O(1) O(V+E) O(E) O(V)
邻接矩阵 O(V2) O(V2) O(1) O(V2) O(1) O(1)

排序算法

下表是排序算法的时间复杂度

算法（用于数组） 最好情况 一般情况 最差情况
冒泡排序 O(n) O(n2) O(n2)
选择排序 O(n2) O(n2) O(n2)
插入排序 O(n) O(n2) O(n2)
归并排序 O(nlog(n)) O(nlog(n)) O(nlog(n))
快速排序 O(nlog(n)) O(nlog(n)) O(n2)
堆排序 O(nlog(n)) O(nlog(n)) O(nlog(n))
桶排序 O(n+k) O(n+k) O(n2)
基数排序 O(nk) O(nk) O(nk)

搜索算法

下表是搜索算法的时间复杂度

算法 数据结构 最差情况
顺序搜索 数组 O(n)
二分搜索 已排序的数组 O(log(n))
深度优先搜索（DPS） 顶点数为V，边数为E的图 O(V+E)
广度优先搜索（BFS） 顶点数为V，边数为E的图 O(V+E)

NP完全理论概述

一般来说，如果一个算法的复杂度为 O(nk)，其中k是常数，我们就认为这个算法是最高效的，这就是多项式算法。

对于给定的问题，如果存在多项式算法，则计为P（polynomial,多项式）。

还有一类NP（nondeterministic polynomial,非确定性多项式）算法。如果一个问题可以在多项式时间内验证是否正确，则计为NP。

如果一个问题存在多项式算法，自然可以在多项式时间内验证其解。因此，所有P都是NP。然而，P = NP 是否成立，仍然不得而知。

小结

我们学习了大O表示法，已经如何运算它计算算法的复杂度。也粗略介绍了NP的一些理论。

书籍链接： 学习JavaScript数据结构与算法

0%